UT logoASE logoCAR logo

Discrete Velocity Gas Dynamics

  • Instantaneous snap shots of the instantaneous density and temperature profiles obtained by the variance reduction method (symbols) compared to time averaged DSMC solutions. The right axis shows the number of sampled collisions in the variance reduction method.
  • Comparison of the moments of the B-K-W distribution for relaxation with and without the interpolation scheme. The interpolation scheme allows for any post-collision velocity to be used while still maintaining conservation of mass, momentum, and energy.
  • The figure shows a comparison of our discrete velocity method with Direct Simulation Monte Carlo using the variable hard sphere collision model. A VHS parameter of ω = 0.78 was used (the value for N-2). The two methods show good agreement in shock thickness when using the variable hard sphere model. It should also be noted how the discrete velocity solution produces smooth results.
  • Discrete representation of the Bobylev-Krook-Wu distribution along z = 0. The grid spacing is uniform and the spacing is β = 0.7. The B-K-W distribution is the only known analytic solution to the Boltzmann equation. It is used for verification of the code after changes have been made.
  • Time variation of entropy and number of collisions, note logarithmic scale for collisions.
  • The figure shows the relaxation of the Maxwellian distribution with an initial translational temperature and no initial rotational temperature. Internal energy is exchanged through the Larsen-Borgnakke model for rotational energy. The relaxation rate is Zr = 5, which controls the number of inelastic collisions (collisions that exchange energy) to elastic collisions (no internal energy exchange).
  • Slice of the Bobylev-Krook-Wu distribution function at z = 0. The B-K-W distribution is the only known analytic solution to the Boltzmann equation. It is used for verification of the code after changes have been made.
  • Relaxation of the 4th, 6th, 8th, and 10th moments of the distribution function.
  • Instantaneous snap shots of the instantaneous density and temperature profiles obtained by the variance reduction method (symbols) compared to time averaged DSMC solutions. The right axis shows the number of sampled collisions in the variance reduction method.
  • Instantaneous snap shots of the instantaneous density and temperature profiles obtained by the variance reduction method (symbols) compared to time averaged DSMC solutions. The right axis shows the number of sampled collisions in the variance reduction method.
  • Slices of the BKW distribution at different times. The square symbols are from the variance reduction method and the triangles are without variance reduction.

The Navier-Stokes (continuum) equations fail to accurately represent a flow when the characteristic length scale for macroscopic gradients is on the same order as the mean free path of the molecules in a gas, and the Boltzmann equation is needed. It remove the continuum constraint and models the gas on a microscopic level through interactions and convection of individual molecules. Such conditions may occur in micro- and nano-scale devices, shocks, satellite attitude control thruster plumes, around satellites in low-earth orbit, and during hypersonic re-entry.

A standard method for modeling a flow on the microscopic level is called Direct Simulation Monte Carlo (DSMC) where individual particles representing a set number of real molecules are tracked. The method is successful under a wide variety of flow conditions, but it has a number of difficulties with complex and transient flows, stochastic noise, trace species, and high level internal energy states.

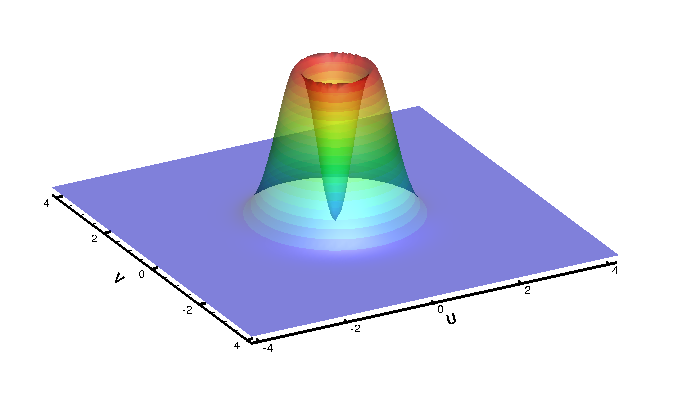
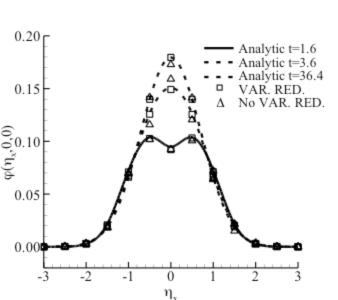
One of the primary goals of this research is to address the concerns with DSMC through the development of an accurate and efficient discrete velocity method for solving the Boltzmann equation. The evolution of a flow is modeled through the collisions and motion of variable mass quasi-particles defined as delta functions on a truncated, discrete velocity domain. The work is an extension of a previous method developed by Aaron Morris, Philip Varghese, and David Goldstein for a single, monatomic species solved on a uniformly spaced velocity grid. The collision integral was computed using a variance reduced stochastic model where the deviation from equilibrium was calculated and operated upon. This method produces fast, smooth solutions of near-equilibrium flows. A 2D representation of the discrete velocity distribution function can be seen in a relaxation of the Bobylev-Krook-Wu distribution (the only analytic, time dependent solution to the Boltzmann equation). Notice that the quasi-particles change size due to collisions but remain at fixed velocity locations (bkw_converted).

Improvements to the method in the current research include:

  • Improved collision cross-section models such as variable hard sphere (VHS) and variable soft sphere (VSS).
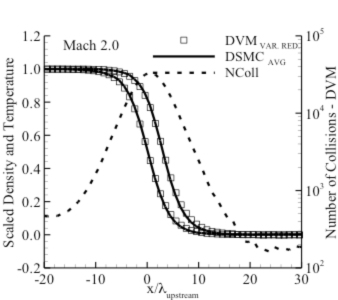
  • Diffuse boundary conditions. Transient solutions to couette flow at Kn=0.1 display an application of the boundary condition.
  • Simple realignment of velocity grid lines into non-uniform grids.
  • Multiple species. Specifically trace species and species with large molecular mass ratios.
  • Quantized rotational and vibrational energy. The evolution of vibrational levels is easily tracked during flow simulations. For instance, in a homogeneous relaxation of kinetic and vibrational temperature (levels), results show smooth instantaneous solutions to vibrational distributions down to O(10E-6) density fraction values. Good resolution of high energy states will be important to future work on chemistry and ionization.

A variance reduced form of each of the improvements has been developed in order to maintain the computational benefits of the method. Each of the improvements allow for more complex or more accurate flow simulations by either expanding the physical complexity of the model or by providing more efficient computations. Some of the major benefits of the method are accurate and smooth representation of rare but important particles such as highly energetic trace species, high energy vibrational states, or the very low densities found at the front of an expansion into vacuum:

vacuum

Funding for this research was provided by NASA and the NSF.