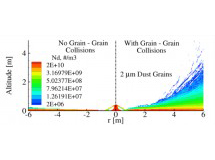
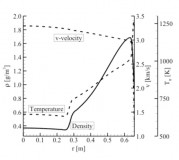
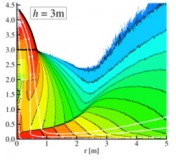
When a rocket lands on the Moon the engine exhaust plume will strike the lunar surface and disturb and disperse dust and larger debris. For any pre-existing structures (or residents) that plume of particulate ejecta represents a significant safety hazard. The scattered particles may penetrate weak surfaces, get stuck in mechanical systems, or coat solar panels, thermal radiators or optical systems. Such debris/dust may be difficult or impossible to clear from surfaces because of electrostatic attractions and the highly adhesive properties of lunar soil. The dust also abrades optical surfaces and space suits, gets into joints, damages seals, and was considered by astronauts John Young and Gene Cernan to be among the most important obstacles to normal lunar operations. Moreover, since there is negligible background atmosphere on the moon, the range of particulate trajectories is very large. Knowledge of the high velocity dust spray will be necessary when making engineering design decisions. However, it is difficult to examine this experimentally because of the difficulties associated with firing rocket engines into a dust bed while maintaining vacuum in a low gravity environment. Therefore, we examine this problem using the direct simulation Monte Carlo (DSMC) method.
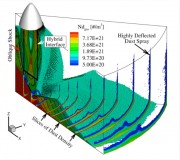
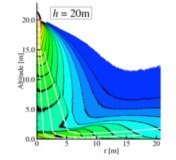
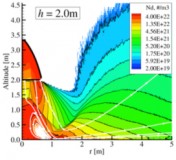
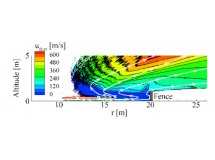
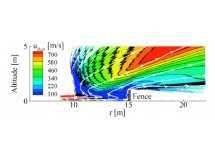
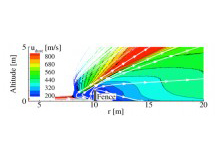
The main objective of this work is to model and characterize the dust sprays that arise during various lunar landing scenarios. The specific landing scenarios modeled in this work include: axisymmetric hover, landing on an inclined surface, and multiple nozzle configurations. We parametrically study the effects that the hovering altitude and engine thrust have on the erosion profiles and the resulting dust sprays. In a multiple engine configuration, we examine the plume-plume interactions and the effects that it has on trenching and dust spray behavior. In addition, high velocity dust sprays are likely unavoidable and can be detrimental to sensitive structures at a nearby lunar outpost. Various mitigation techniques, such as a fence, have been proposed to shield nearby structures from the dust spray. To assess the effectiveness of such a fence, the interaction between the high velocity dust spray with the fence is also studied. To accomplish these tasks, we first model the plume flow field using a hybrid continuum–DSMC solver that is computationally efficient in the continuum near field and also accurate as the flow transitions towards rarefied and free molecular flow. The surface stresses are computed and used to determine the dust erosion rate. A two–phase flow model is then used to determine the trajectories of the entrained dust grains. Once entrained into the flow, the effects of dust particle collisions are also studied. This work will aid in the design of future lunar landers by describing how the dust sprays respond for different weight landers and engine configurations. The high velocity dust sprays may be unavoidable without a pre-established landing platform. Mitigation structures, such as a fence or berm, may be necessary to protect any establishments on the moon. Our models can aid in the design of such a fence by predicting the impingement stresses and how the dust spray will respond.
- Plume Impingement on a Dusty Lunar Surface
- Modeling The Interaction Between a Rocket Plume, Scoured Regolith, and a Plume Deflection Fence
- Far Field Deposition of Scoured Regolith Resulting from Lunar Landings
- Simulation of Rocket Plume Impingement and Dust Dispersal on the Lunar Surface – Dissertation